移動平均線とは、Moving Averageとも呼ばれるテクニカル指標です。
数あるテクニカル指標の中で最もポピュラーと言っても過言ではないほど有名で、重要です。
多くのトレーダーが活用しているためテクニカル指標通りに為替レートが動きやすいのが特徴です。
初心者のトレーダーはもちろん、上級者のトレーダーも要チェックと言えるでしょう。
- 移動平均線とはどんなテクニカル指標か
- 移動平均線でよく使われる期間
- 移動平均線で読み取れる情報
- 移動平均線の種類
目次 表示
移動平均線とは
移動平均線は、ある一定期間における終値の平均値をつなぎ合わせたものです。
為替レートは、価格が上昇したり下落したりを繰り返しています。
価格が上昇傾向にある場合でもローソク足が陰線になることや、下落傾向にある場合にローソク足の陽線が出現することは珍しくありません。
移動平均線は、終値を平均化することによって価格のダマシをなだらかにし、情報を読み取りやすくする効果があります。
移動平均線でよく使われる期間
移動平均線で使用する期間は、トレードスタイルによって適切な期間が異なります。
- 200本分の移動平均線⇒数か月~数年の価格動向が見れるので長期売買向け
- 20本分の移動平均線⇒数時間~数日の価格動向が見れるので短期売買向け
また、指標の分析方法によっても選択する期間が異なる場合もあります。
- パーフェクトオーダーを確認したいので、短期/中期/長期の期間を選択
- 5分足チャートで15分足20本分の移動平均線を疑似的に確認したいので、60本を選択
さらには、このように「意識しやすい数字」を期間の数値として選択しているトレーダーもいます。
- フィボナッチ数列に含まれる数字
- キリのいい数字
- 1週間の営業日(5日)や約3か月(13週)などの「区切り」を意識した数字
トレードスタイルや指標の分析方法に合わせて、適切な期間を選択しましょう。
よく使われる期間をまとめました。参考にしていただければと思います。
| 時間軸 | よく使われる期間 |
|---|---|
| 分足 時間足 |
5、20、25、50、75、100、200 |
| 日足 | 5、25、75、200 |
| 週足 | 13、26、52 |
| 月足 | 12、24 |
移動平均線で分かること
移動平均線で分かることは、以下のようなものがあります。
- トレンドか否か
- 強いトレンドかどうか
- 相場の転換ポイント
複数のテクニカル指標と組み合わせて、より詳しい相場分析をすることが重要です。
 はちわれ
はちわれ
トレンドか否か
為替レート(ローソク足)を平均化したものが移動平均線です。
そのため、「移動平均線から為替レート(ローソク足)が離れている時は買い圧力と売り圧力の均衡が崩れている可能性がある」と考えることができます。
移動平均線の上を為替レートが推移している場合、「買いの圧力が強い=上昇トレンドの可能性」と分析することができます。
また、移動平均線の下を為替レートが推移しているならば、「売りの圧力が強い=下降トレンドの可能性」と分析できます。
移動平均線から一時的に為替レートが離れているだけの時もありますが、トレンドが発生していると判断する材料の一つになる場合があります。
- 移動平均線から為替レート(ローソク足)が離れている時、トレンドが発生している可能性が高い
- 移動平均線と為替レートが重なっているならば、買いと売りの圧力が均衡している=レンジ相場と考えられる
強いトレンドかどうか
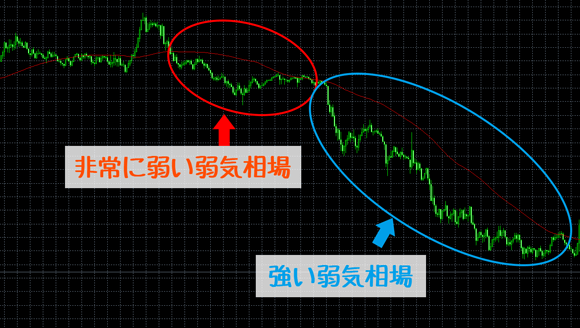
為替レートを平均化させている移動平均線は、あまり激しい動きにはならない傾向にあります。
その移動平均線が大きく上昇しているということは、価格レートも上下動はあれど平均して大きく上昇していると考えられます。
また、その逆も然りです。
つまり、移動平均線が大きく上昇/下降している場合、強いトレンドが発生している可能性があると分析することができます。
この考え方から、移動平均線の傾き(角度)を指標として表すインジケーターを利用しているトレーダーもいます。
- 動きがなだらかな移動平均線が大きく上昇/下降している場合、強いトレンドが発生している可能性がある
相場の転換ポイント
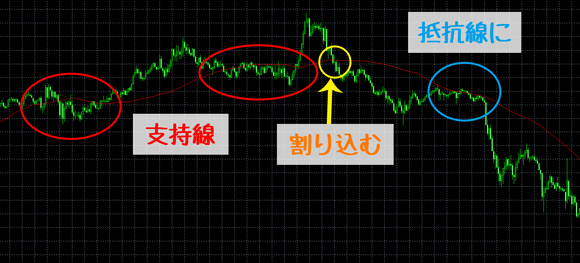
移動平均線は、時には支持線(サポートライン)や抵抗線(レジスタンスライン)の役割を担う場合があります。
支持線や抵抗線は、「支持線を為替レートが割り込む(抵抗線を為替レートが上回る)と、相場の転換のポイントとなる」場合があります。
これは、「支持線を割り込んだので、さらに為替レートが下がる可能性がある」「抵抗線を上回ったので、買いの圧力が強くなるであろう」といったトレーダーの意識が働くからです。
つまり、支持線(サポートライン)や抵抗線(レジスタンスライン)の役割を担っている移動平均線を為替レートが割り込んだり上回ったりした場合、相場の転換が起こる可能性があると考えられます。
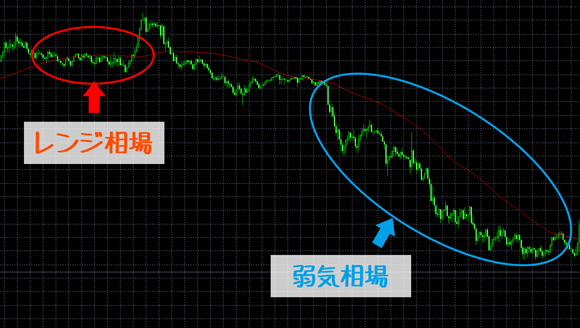
- 支持線の役割を担っていた移動平均線を為替レート(ローソク足)が割り込んだ場合、弱気相場に転換する可能性がある
- 抵抗線の役割を担っていた移動平均線を為替レート(ローソク足)が上回った場合、強気相場に転換する可能性がある
移動平均線の種類
移動平均線には様々な種類があります。
平均する方法が異なっているため、各移動平均線ごとに特徴や強みが異なります。
トレード手法や分析したい事柄を明確にして、適切な移動平均線を用いましょう。
 はちわれ
はちわれ
参考
Moving Average(移動平均)MetaTrader 5のヘルプ
単純移動平均線(Simple Moving Average、SMA)
単純移動平均線は、一番シンプルな移動平均線です。
ある一定期間の終値を単純に足して平均化した移動平均線です。
計算式
SMA[0] = (終値[0]+終値[1]+終値[2]+…+終値[x-1]) / x
備考
SMA[0]:当日のSMA
終値[0]:当日の終値
終値[1]:1日前の終値
x:期間
平滑移動平均線(Smoothed Moving Average、SMMA)
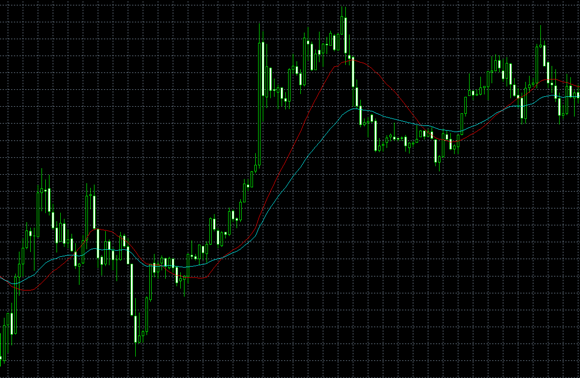
赤:単純移動平均線
青:平滑移動平均線
平滑移動平均線は、単純移動平均線を改良した移動平均線です。
単純移動平均線は、期間外の過去の値動きは計算に含まれません。
そのため、計算から外れる終値と直近の終値の価格差によっては、「直近の終値は下降傾向にあるのに、移動平均線は上昇した」といった状況も発生します。
平滑移動平均線では、計算から外れる終値も計算に含まれるような算出方法になっています。
そのため、単純移動平均線よりも滑らかな移動平均線になっています。
しかし、過去の値動きも含めて計算するため、反応が鈍いというリスクも抱えています。
計算式
SMMA[0] = (SMMA[1] × (x-1) + 当日の終値) / x
備考
SMMA[0]:当日のSMMA
SMMA[1]:前日のSMMA
1日目の前日のSMMAは、x日単純移動平均とする。
終値[0]:当日の終値
終値[1]:1日前の終値
x:期間
指数移動平均線(Exponential Moving Average、EMA)
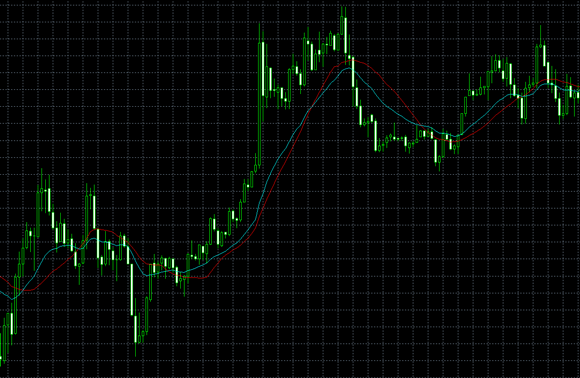
赤:単純移動平均線
青:指数移動平均線
指数移動平均線は、平滑移動平均線を改良し直近の価格に重きを置いた移動平均線です。
平滑移動平均線と同様に期間外の過去の値動きも計算に含まれていくので、滑らかな移動平均線になります。
また、直近の価格を2倍の数値にして平均化するので、直近の価格変動に敏感に反応します。
その分、単純移動平均線よりダマシが発生しやすくなるというリスクも抱えています。
計算式
EMA[0] = (終値[0]+終値[0]+終値[1]+終値[2]+…+終値[x-1]) / (x+1)
このように置き換えることもできます。
EMA[0] = (EMA[1] × (x-1) + 当日の終値 × 2) / (x+1)
備考
EMA[0]:当日のEMA
EMA[1]:前日のEMA
1日目の前日のEMAは、x日単純移動平均とする。
終値[0]:当日の終値
終値[1]:1日前の終値
x:期間
線形加重移動平均線(Linear Weighted Moving Average、LWMA)
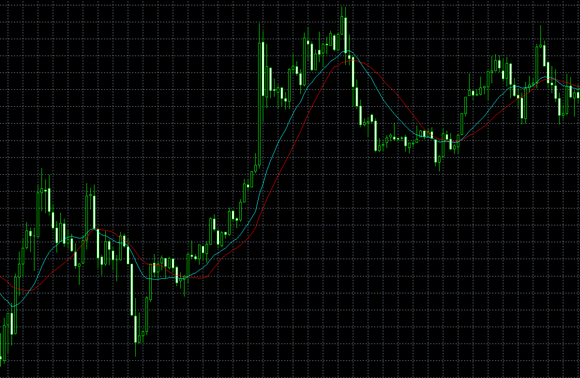
赤:単純移動平均線
青:線形加重移動平均線
線形加重移動平均線は、過去の価格から直近の価格の方向に徐々に重きを置く計算方法となっています。
直近の価格に重きを置く考え方は指数移動平均線や平滑移動平均線と同様ですが、重きの置き方が異なります。
そのため、線形加重移動平均線は「緩やかな上昇相場/下降相場」に対して明確な描画を行います。
半面、動きがあまりない「レンジ相場」や、大きな変化のある「強いトレンド相場」には弱く、遅れて弱く反応する傾向にあります。
計算式
LWMA[0] = [(終値[0] × x) + {終値[1] × (x – 1)} + {終値[2] × (x – 2)} + …… + {終値[x-2] × 2} + 終値[x-1] / {(x + (x – 1) + (x – 2) + …… + 2 + 1)}
備考
LWMA[0]:当日のLWMA
終値[0]:当日の終値
終値[1]:1日前の終値
x:期間
適応型移動平均線(Adaptive Moving Average、AMA)
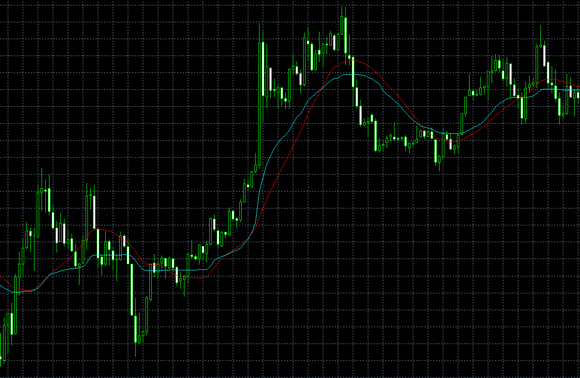
赤:単純移動平均線
青:適応型移動平均線
適応型移動平均線は、Perry Kaufmanによって開発された移動平均線です。
通常の移動平均線は、一時的に為替レートが大きく変動しただけの場合でも反応を示してしまいます。
また、平滑化しているのでトレンド発生時に反応が鈍く、シグナルが示された時点では既に時遅し、という場合も少なくありません。
適応型移動平均線は、これらの2つの欠点を克服するために開発されたインジケーターです。
計算式
Signal[0] = |(終値[0] – 終値[x])|
Noise[0] = |(終値[0] – 終値[1])| + |(終値[1] – 終値[2])| +…+ |(終値[x-1] – 終値[x])|
ER[0] = Signal[0] / Noise[0] SC = 2 / (x + 1)
SSC[0] = (ER[0] × (高速SC – 低速SC)) + 低速SC
AMA[0] = 終値[0] × SSC[0]の2乗 + AMA[1] × (1 – SSC[0]の2乗)
備考
AMA[0]:当日のAMA
AMA[1]:前日のAMA
1日目の前日のAMAは、x日単純移動平均とする。
終値[0]:当日の終値
終値[1]:1日前の終値
Signal[0]:当日のSignal
Noise[0]:当日のNoise
ER[0]:当日のER
x:期間
ハル移動平均線(The Hull’s Moving Average、HMA)
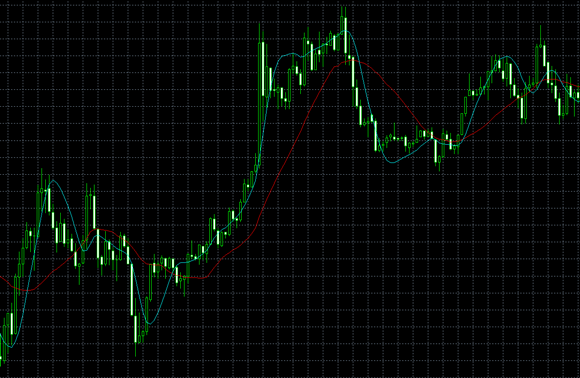
赤:単純移動平均線
青:ハル移動平均線
ハル移動平均線は、Alan Hullによって開発された移動平均線です。
2本の加重移動平均線を用いて計算する移動平均線で、価格変動に非常に敏感に反応する点が特徴です。
相場の変動に対して非常に敏感な反応を示すので、トレンド判定には不向きと言えるでしょう。
計算式
value(x) = 2 × LWMA(x/2) – LWMA(x)
HMA(x) = LWMA(√x,value)
備考
value(x):期間xの値value
LWMA(x/2):期間x/2の線形加重移動平均
LWMA(x):期間xの線形加重移動平均
HMA(x):期間xのHMA
LWMA(√x,value):値valueを期間√xで線形加重移動平均
x:期間
2重指数移動平均線(Double Exponential Moving Average、DEMA)
2重指数移動平均線は、Patrick Mulloyによって開発された移動平均線です。
相場が不安定な際のノイズを減らしつつ、価格変動に対する反応が良い移動平均線です。
計算式
err[0] = 終値[0] – EMA[0](x)
ema[0] = EMA[0](x)
DEMA[0] = EMA[0](x) + EMA[0](x,err)
= 2 × EMA[0](x) – EMA[0](x,ema)
備考
err[0]:当日のerr
終値[0]:当日の終値
ema[0]:当日のema
DEMA[0]:当日のDEMA
EMA[0](x,err):値errを期間xで指数移動平均
EMA[0](x,ema):値emaを期間xで指数移動平均
x:期間
フラクタル適応型移動平均線(Fractal Adaptive Moving Average、FRAMA)
フラクタル適応型移動平均線は、John Ehlersが開発した移動平均線です。
フラクタル次元を元にして、計算時に毎回指数平滑係数を計算します。
フラクタル次元がもとになっているので、直線的な価格変動の際は実際の価格変動に近い平均値を示します。
ギザギザで安定しない価格変動の際は、平滑係数が極端に小さい値に変化するため、動きの小さいグラフ曲線になります。
計算式
A[0] = Exp(-4.6 * (D[0] -1))
D[0] = (Log(N1 + N2) – Log(N3))/Log(2)
N[0](y) = (Highest終値[0] – Lowest終値[0]) / y
N1(0) = N[0](y)
N2(0) = N[y](y)
N3(0) = N[0](2y)
FRAMA[0] = A[0] × 終値[0] + (1 – A[0]) × FRAMA[1]
備考
A[0]:当日のA
Exp():e(ネイピア数)のべき乗値
D[0]:当日のD
Log():対数
N[0](y):y期間を対象とした当日のN
FRAMA[0]:当日のFRAMA
x、y:期間
3重指数移動平均線(Triple Exponential Moving Average、TEMA)
3重指数移動平均線は、Patrick Mulloyが開発した移動平均線です。
指数移動平均線よりも反応が早く、ノイズの少ないグラフ曲線を描きます。
価格や指標の平滑化に利用されます。
計算式
err[0] = 終値[0] – DEMA[0](x)
ema[0] = EMA[0](x)
ema2[0] = EMA[0](x,ema)
TEMA[0] = DEMA[0](x) + EMA[0](x,err)
= 3 × EMA[0](x) – 3 × EMA[0](x,ema) + EMA[0](x,ema2)
備考
err[0]:当日のerr
終値[0]:当日の終値
ema[0]:当日のema
ema2[0]:当日のema2
DEMA[0](x):期間xにおける当日のDEMA
TEMA[0]:当日のTEMA
EMA[0](x,err):値errを期間xで指数移動平均
EMA[0](x,ema):値emaを期間xで指数移動平均
EMA[0](x,ema2):値ema2を期間xで指数移動平均
x:期間
可変インデックス動的平均線(Variable Index Dynamic Average Technical Indicator、VIDYA)
可変インデックス動的平均線は、Tushar Chandeによって開発された移動平均線です。
相場のボラティリティに応じて変更した平均期間で指数移動平均します。
ボラティリティが高い場合に価格変動を重視するグラフ曲線を描くので、トレンド判定に強い移動平均線と言えます。
計算式
F = 2 / (x + 1)
CMO[0] = (CMOup[0] – CMOdown[0]) / (CMOup[0] + CMOdown[0])
VIDYA[0] = VIDYA[1] + (F × |CMO[0]|) × (終値[0] – VIDYA[1])
備考
F:平滑化係数
CMO[0]:当日のCMO
|CMO[0]|:当日のCMOの絶対値
CMOup[0]:期間x間で前日比+とした足の値幅合計
CMOdown[0]:期間x間で前日比-とした足の値幅合計
VIDYA[0]:当日のVIDYA
VIDYA[1]:前日日のVIDYA
終値[0]:当日の終値
x:期間
移動平均線の種類や特徴 まとめ
いかがでしたでしょうか。移動平均線には、とてもたくさんの種類があります。
移動平均線ごとに得意な相場が異なり、描画にも特徴があります。
自分のトレードスタイルや欲しい情報に合わせて利用しましょう。